Métodos numéricos calculo de areas

Métodos numéricos

Calculo de Integrales mediante metodos númericos

Regla del rectángulo

El método más simple de este tipo es hacer a la función interpoladora ser una función constante (un polinomio de orden cero) que pasa a través del punto (a,f(a)). Este método se llama la regla del rectángulo: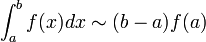

Regla del punto medio

Ilustración de la regla del punto medio.

Si en el método anterior la función pasa a través del punto regla del punto medio: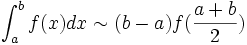

Regla del trapecio

Ilustración de la regla del trapecio.

La función interpoladora puede ser una función afín (un polinomio de grado 1 o sea una recta) que pasa a través de los puntos regla del trapecio: