Algunos ejercicios de Métodos numéricos

Encuentra la raíz en el intervalo [0,3] de la función 

Utilizando el método de la bisección, y el método de Newton

Como funciona las notas de los parciales y los Finales

Para calcular la nota Final
Cada parcial cuenta un 15% de la nota, siempre que la nota del parcial sirva para subir la nota total.

Es decir la nota de cada parcial cuenta ese 15%, si la nota del parcial es superior a la nota del examen final

Recordamos las preguntas que saldrán en el final

Final del día 29 (Sábado) de Enero del 2010

1. Factorización LU
2. Ecuaciones diferenciales. Movimiento o Población.
3. Áreas o Volúmenes (integrales)
4. Derivadas de 1 variables
5. Derivadas de 3 variables
6. Gauss Jordan
7. Máximos y Mínimos de funciones de 2 Variables: "Hessiana"
8. Métodos Numéricos

Parciales Corregidos

Ya he corregido el 3º Parcial.

Podéis pasar a recogerlo Lunes 24 a las 9:30 por mi despacho en Salesa.

El despacho esta en la 1º Planta, muy cercano a la cafetería.

Apuntes del día 17-1-2011

Gracias a Andres Hernandez

Apuntes día 20-12-10

Gracias a Ángela Arce





Para descargar
Para descargar2

Macro Tutoria para prepara el examen Final

He reservado el Aula 1.2 para hacer una tutoria el Jueves 27 a las 9:00 para resolver las dudas que tengáis antes del examen.

Problemas de Máximos y Mínimos, y Métodos Numéricos

1º Ejercicio

 Encuentra la raíz por Métodos numéricos de la función, en el intervalo [0,3], 

1º Método de bisección 3 interacciones. (3 pasos)

2º Método de Newton 3 iteracciones (3 pasos)

2º Ejercicio 

Calcula el área encerrada  en el intervalo [0,1]

1º) Método del rectángulo, a) con un intervalo, b) con dos intervalos

2º) Método de punto medio   a) con un intervalo, b) con dos intervalos

3º) Método del trapecio  a) con un intervalo, b) con dos intervalos

3º Ejercicio 

Busca los Máximos y Mínimos de la siguiente función de 2 variables 

4º Ejercicio 

Busca los Máximos y Mínimos de la siguiente función de 2 variables

Los apuntes del día 11 gracias a Raquel

Métodos numéricos calculo de areas

Métodos numéricos

Calculo de Integrales mediante metodos númericos

Regla del rectángulo

El método más simple de este tipo es hacer a la función interpoladora ser una función constante (un polinomio de orden cero) que pasa a través del punto (a,f(a)). Este método se llama la regla del rectángulo: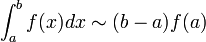

Regla del punto medio

Ilustración de la regla del punto medio.

Si en el método anterior la función pasa a través del punto regla del punto medio: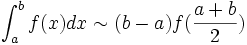

Regla del trapecio

Ilustración de la regla del trapecio.

La función interpoladora puede ser una función afín (un polinomio de grado 1 o sea una recta) que pasa a través de los puntos regla del trapecio:

Métodos numéricos búsqueda de raíces

Métodos numéricos

La disciplina ocupada de describir, analizar y crear algoritmos numéricos que nos permitan resolver problemas matemáticos, en los que estén involucradas cantidades numéricas

En el contexto del cálculo numérico, un algoritmo es un procedimiento que nos puede llevar a una solución aproximada de un problema mediante un número finito de pasos que pueden ejecutarse de manera lógica.

A partir de aquí, aparece un concepto adicional, el de error.

Búsqueda de raíces

En análisis numérico un algoritmo de búsqueda de raíces es un método numérico o algoritmo para encontrar las soluciones aproximadas de una ecuación dada por la expresión f(x) = 0 para una función matemática f dada. A la solución x de la ecuación se le llama raíz o cero de la función.

El algoritmo más simple de búsqueda de raíces es el método de bisección. Requiere un intervalo inicial que contenga alguna raíz de la ecuación (de forma que la función tome en los extremos del mismo valores de distinto signo; véase el teorema de Bolzano). Dicho intervalo inicial se va dividiendo sucesivamente por la mitad (se bisecta) tomándose el intervalo que contiene a la raíz. A pesar de ser un método que siempre converge a una solución, converge muy lentamente.

http://es.wikipedia.org/wiki/M%C3%A9todo_de_bisecci%C3%B3n

Ejemplo función:  

f(x)=x^2-1  Entre el 0 y 3

Ejemplo función:

f(x)=x^2+x-1  Entre 0 y 1

Es un algoritmo seguro pero lento

Uno mejor: Método de Newton

http://es.wikipedia.org/wiki/M%C3%A9todo_de_Newton

Ejemplo función  

f(x)=x^2-1  Entre el 0 y 3

Ejemplo función

f(x)=x^2+x-1  Entre 0 y 1

Preguntas para el Parcial y para el Final

Parcial Día 18-1-2010 a las 9:00 en el aula 1.2

Preguntas.

1. Métodos numéricos
2. Máximos y Mínimos de funciones de 2 Variables: "Hessiana"
3. Factorización LU
4. Ecuaciones diferenciales. Movimiento o Población.
5. Áreas o Volúmenes (integrales) 
6. Gauss-Jordan

Final del día 29 (Sábado) de Enero del 2010

1. Factorización LU
2. Ecuaciones diferenciales. Movimiento o Población.
3. Áreas o Volúmenes (integrales) 
4. Derivadas de 1 variables
5. Derivadas de 3 variables
6. Gauss Jordan
7. Máximos y Mínimos de funciones de 2 Variables: "Hessiana"
8. Métodos Numéricos

Ejercicios de Máximos y Mínimos de funciones de dos variables

En esta función me salen 4 puntos candidatos.

Apuntes del 10-1-2011

Para descargar

Gracias a Jonathan Vivancos

Clase del 10 de Diciembre del 2010

1º Reparto de Parciales

2º Máximos, Mínimos y Puntos de Inflexión para funciones de 2 variables.
(Matriz Hessiana, "Hessianitos")

Para el próximo día 11 de Diciembre: Métodos Numéricos.

El 17 de Diciembre clase de Repaso, y centrar las preguntas de los parciales, y del final

El 18 de Diciembre 3º y ultimo parcial.


EL 24 de DICIEMBRE, cita a las 9:30 en el despacho de Matemáticas de la planta baja. Para repartir los parciales.

Nota: El delgado conoce donde esta el despacho.

Próxima clase día 10 de Enero del 2011

En la próxima clase del día 10 de Enero del 2011

Repartiremos los parciales corregidos. Y nos adentraremos al mundo de los máximos y mínimos de funciones de varias variables.